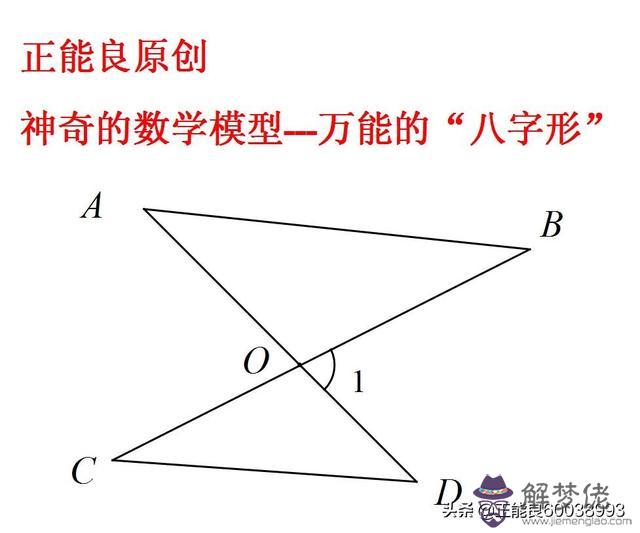
神奇的模型數學（21）---萬能的“八字形”問題提出：
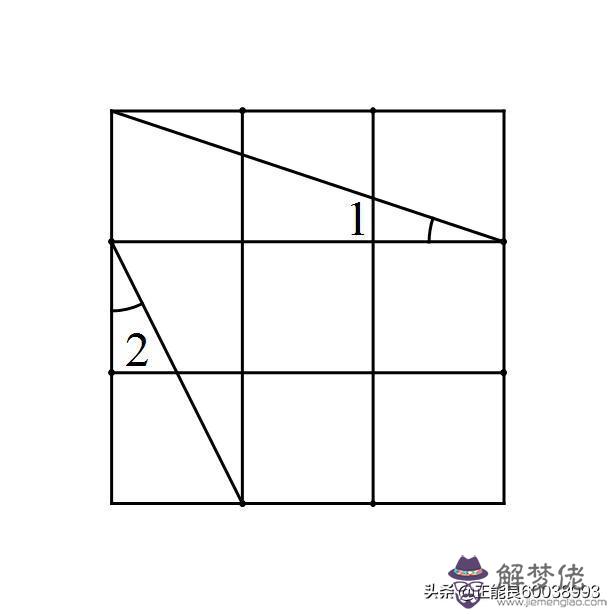
如圖，在3×3的正方形網格中標出了∠1和∠2.則∠1+∠2=___.
首先讓我們來看一個大家再熟悉不過的題：
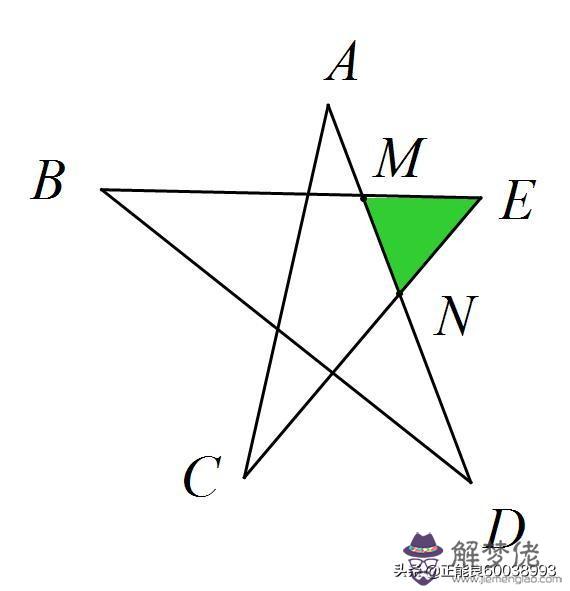
如圖，已知五角星ABCDE，試求∠A+∠B+∠C+∠D+∠E的度數。
∵∠ENM是△ACN的外角,
∴∠ENM=∠A+∠C,(三角形的外角等于不相鄰的兩個內角的和)
同理可得,∠EMN=∠B+∠D.
∵∠MNE+∠NME+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°
在n年前我的老師是這樣教我們的,若干年后正能良傳承了老師的衣缽,我也一直是這樣教自己的學生.想必大家與我一樣認為這就是唯一的解法.這的確是一種好的數學方法，運用了轉化的數學思想，把要求的"五角星”的五個角的和集中到一個三角形中.也許就是因為這種解法太過完美了,一直把我們的思維禁錮其中,以致于一丁點都沒有去思考過有沒有更巧妙的方法.一次正能良在做類似的題的時候突然眼前一亮,發現了一個對于解決角度和的問題萬能的數學模型---"八字形".
數學模型：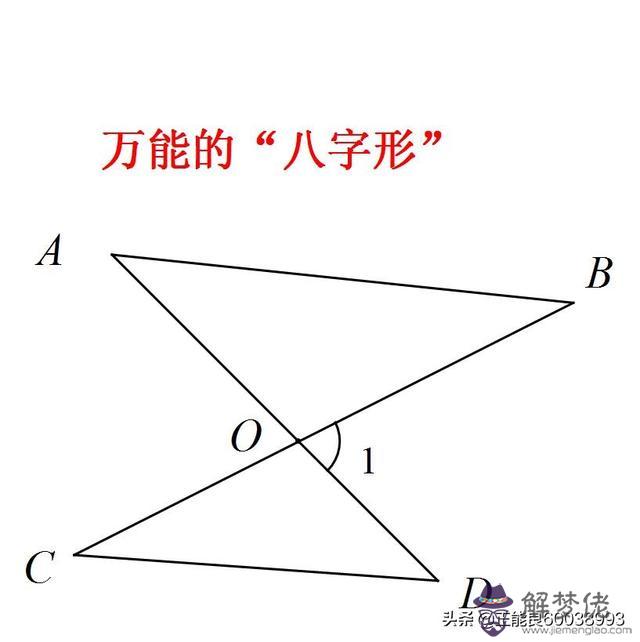
內涵:∠A+∠B=∠C+∠D.事實上,根據三角形的外角等于不相鄰的兩個內角的和可得,∠A+∠B=∠1,∠C+∠D=∠1,所以有∠A+∠B=∠C+∠D.
下面我們用萬能的“八字形”來解決五角星問題:
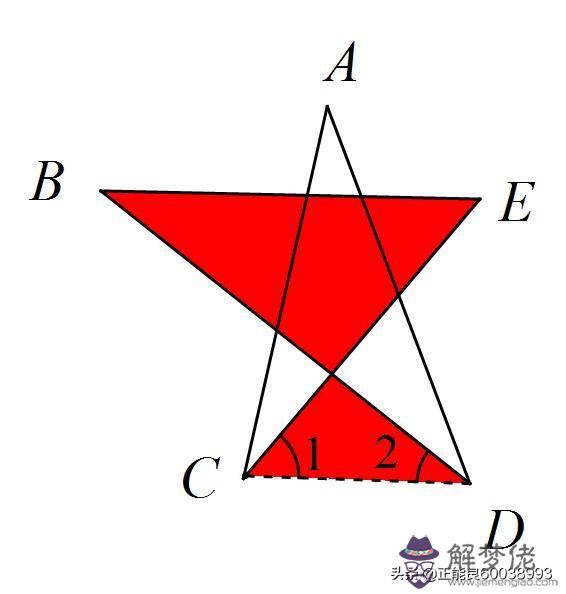
解：如圖，連接CD，
∵∠B+∠E=∠1+∠2，
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠1+∠ACE+∠2+∠ADB
=∠A+∠ACD+∠ADC
=180°.
問題解決：如圖，在3×3的正方形網格中標出了∠1和∠2.則∠1+∠2=___.
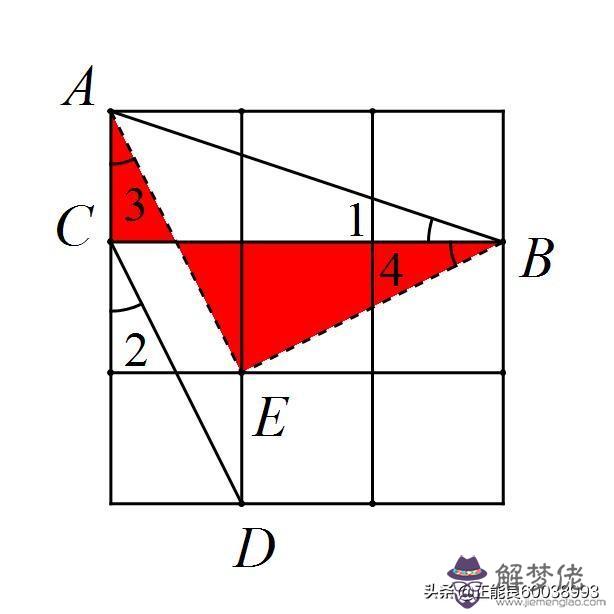
解:連AE,BE,
∵AE∥CD,
∴∠2=∠3.
易知,△ABE為等腰直角三角形,∠AEB=90°,
又∠ACB=90°,
由“八字形”數學模型知,∠3=∠4
∴∠2=∠4.
∴∠1+∠2=∠1+∠4=∠ABE=45°
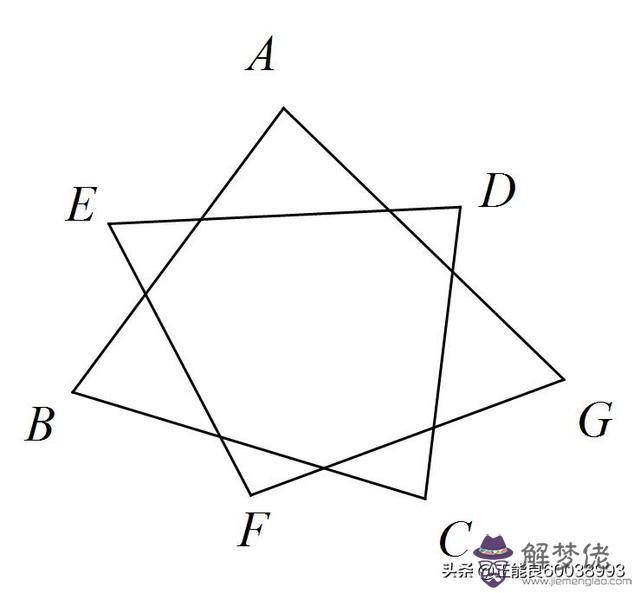
鞏固練習：1.如圖，∠A+∠B+∠C+∠D+∠E+∠F+∠G=（ ）.
A. 540° B. 720° C. 360° D. 900°
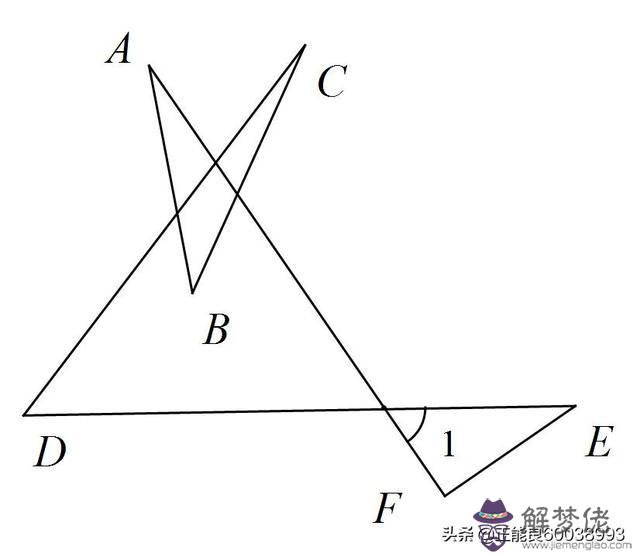
2.如圖,已知∠1=60°,則∠A+∠B+∠C+∠D+∠E+∠F= .
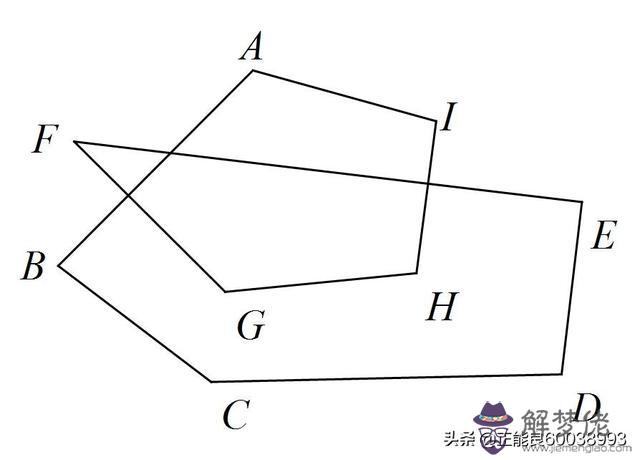
3.如圖，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的度數.
敬請關注：正能良60038993. 本文來自：解夢佬，原地址：https://www.jiemenglao.com/suanming/443902.html
