3月23日出生的人暗示著什麼
出品:科普中國
:李瑞(大阪大學 )
監制:中國計算機 絡信息中心
3月15日是什麼日子?
是消費者權益日,不僅如此,很多名人都出生在這一天,例如清順治帝、德國免疫學奠基人埃米爾·阿道夫·馮·貝林、法國天文學家尼可拉··拉卡伊、中國第六代導演領軍人物之一婁燁等。
跟這麼多名人在同一天生日,是不是特別的緣分,是不是在暗示什麼! 絡上還說遇到和自己同一天生日的人要格外珍惜,出生在同一天是不是有特殊的含義呢!
其實,兩個人在同一天出生的概率可能比你想象的要大很多。
:699pic.com
一個班級中,出現相同生日的概率有多大?
假設某小學某個班級有學生40人,其中出現相同生日(同月同日)的概率有多大?
這其實是一個排列組合的問題。首先,假定同日出生的情況確實存在,那麼可能的組合除了最簡單的一種——兩個人出生在同一天,還會有很多種。
不同日期都存在生日相同的情況,比如兩個人出生在3月15日,兩個人出生在4月13日。可能同一天出生的人不止兩個,例如3月15日出生的人有三個。
這樣考慮起來的話,還可能出現三個人出生在某一天,四個人出生在另外一天之類的復雜情況。
如果想要列舉每個可能的組合,再把概率相加,事實上幾乎是不可能完成的任務。
不過,假如從反面進行思考,這個問題就會變得簡單很多。
同一個班級有重復生日和沒有重復生日這兩個發生的概率相加為1,只要計算出沒有出現生日重復的概率,再用1減去這一概率就是我們想要的結論。
如此一來,我們可以將問題簡化成一個40人的小學班級中沒有任何兩個(或者更多)人出生在同一天的概率。

:699pic.com
為了便利,我們假定先把所有人請室外面,然后再挨個把同學們叫回來,并在這一過程中計算新加入同學和之前同學的生日都不相同的概率。
假設之一位進教室的同學生日是3月15日,我們請第二位同學進場,為了滿足題目的要求,第二位同學的生日可以是365天中除了3月15日的任何一天,與之一位同學生日不相同的概率是364/365。
(這里我們做了兩個假定,之一是不考慮閏年的情況,第二是全年每天的出生率應該均等。)
請第三位同學入場,他的生日不能和之前兩位同學一樣,那麼現在概率就變成了(364/365)×(363/365),之一個括號是前兩位同學生日不相同的概率,第二個括號是第三位和前兩位生日不同的概率,相乘的結果就是三人生日都不同的概率。四個人生日不同的概率就是(364/365)×(363/365)×(362/365)……
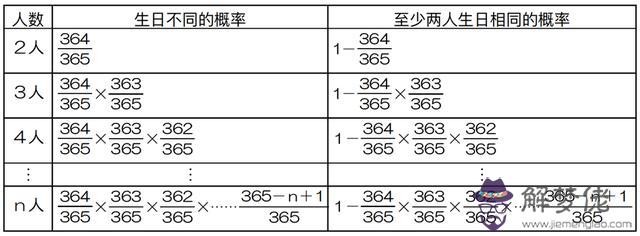
:
以此類推,一直計算到第40個人,再用1來減去算出的概率,就是我們想知道的問題答案,也就是40個人中出現生日重復的概率。
最后得到的結果是89.1%。是不是比預想的要大?
如果人數繼續增加,這個概率還會急劇上升,50個人班級的這一概率是97.0%,60個人則達到99.4%,70個人已經是99.9%。
換句話說,70個人的班級內沒有任何生日相同情況出現的概率小于千分之一。
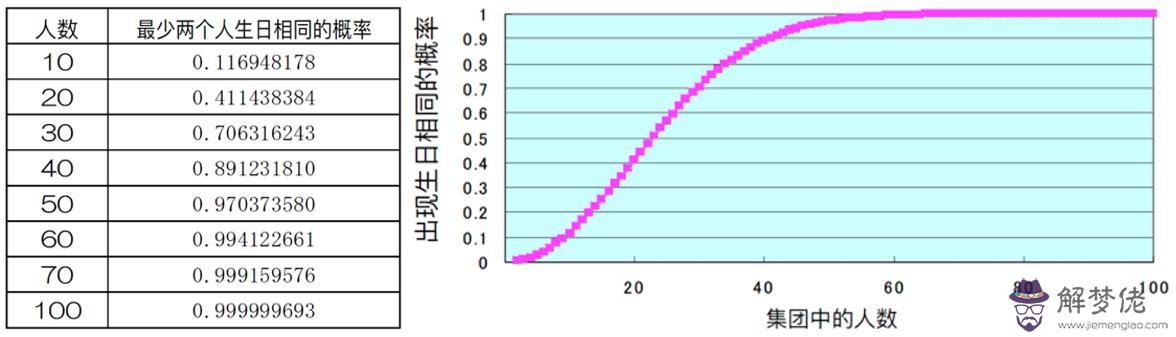
:
小貼士:實際過程中我們無需傻傻地計算三四十次,計算機軟件(簡單的電子表格即可)能幫助我們完成這種重復繁瑣的任務。
有一個非常經典的數學”悖論”叫做”生日問題”:在一個房間最少要多少人,可以讓其中兩個人生日相同的概率大于50%?
根據上面的計算,我們可以很容易地得到答案,23個人。
相信這一數字比大多數人的直覺預估都要少。
雖然稱為”悖論”,但從引起邏輯矛盾的角度來說生日問題并不是悖論,它被稱作悖論只是因為這個數學事實與一般直覺相抵觸而已。
畢竟大多數人會認為,23人中有2人生日相同的概率應該遠遠小于50%。
遇到和自己同一天生日的人概率有多大?
說到這里,你可能會有一個疑惑:既然上面算出的概率都大得出乎意料,那為什麼自己從小到大都沒在班級中遇到和自己同天出生的人?
其實,如果你足夠聰明,應該會意識到這是另外的一個命題——一個40人的班級中,出現和自己同天生日人的概率是多少?

:699pic.com
我們還是用逐一請同學們進教室的思考方式解答問題。先計算40人班級中沒有任何一個人跟自己生日相同的概率,再用1減去這個值,就是我們需要的結果。
首先”我”進入教室,第二個進入教室的同學生日和”我”不同的概率是364/365,第二、第三個同學生日和”我”都不同的概率是(364/365)×(364/365),進入第四個同學時的答案是(364/365)×(364/365)×(364/365)……
以此類推,當進入第n個同學的時,概率是(364/365)的n-1次方。
最后,我們再用1減去上面的結果,就是n個人的班級中,出現和自己同一天生日的人的概率。
計算結果如下:4個人的班級(0.8%)、23個人的班級(5.8%)、40個人的班級(10.1%)……
結果來看比上一個問題更加合我們的普遍認知。
所以40個人的班級中,出現和自己生日相同同學的概率是10.1%。
我們每個人從小到大都會加入很多班級,從以上的計算結果來看,假如從小到大任何一個班級中都沒有生日相同的人,那才是真正的奇跡!
我們以小學每個班60人,初中每個班70人,高中每個班50人,大學每個班30人進行計算,結果是小于一千萬分之五,概率上來說已經到了大獎的級別。
所以,一群人中出現生日相同的概率就已經比很多人的預想要大得多,更不用說全球幾十億人了。
當然,由于實際上每天的出生率并沒有顯著差別,全球70億人中,某個日期(注意是日期不是具體的年份加日期,如3月15日,而非1985年3月15日)對應的人口總數大約是2000萬。
如果再考慮歷史上已經死去的人,那某天出生的人必然都是天文數字,其中的任何一天都有無數的名人出生或者故去。
這麼說來,雖然我們希望每一天都是美好、特別、神奇的日子,不過其實每一天都平凡而普通。

以上就是與3月23日出生的人暗示著什麼相關內容,是關于概率計算的分享。看完九月九出生有緣后,希望這對大家有所幫助!
本文來自:解夢佬,原地址:https://www.jiemenglao.com/suanming/413313.html

















