怎樣判斷函數開口向上還是向下
二次函數圖象的說法:
二次函數y=ax²+bx+c的圖像是一個拋物線,所以也可以說“拋物線y=ax²+bx+c”,這兩種說法沒什麼不同,你喜歡哪種就用哪種。
接下來說說如何判斷二次函數表達式中的常數“a、b、c”號。
如何判斷a號:
a大于0時,拋物線開口向上,反之也成立;a小于0時,拋物線開口向下,反之也成立。所以a號通常是根據拋物線的開口方向確定的。
如何判斷b號:
b存在于拋物線的對稱軸x=-b/2a中,所以一般根據對稱軸號來判斷b號。
例如:已知拋物線開口向上,對稱軸在x軸的左側,判斷b號:
拋物線開口向上,則a>0;對稱軸在x軸左側,則-b/2a<0;很容易得出b>0。
如何判斷c號:
對于二次函數y=ax²+bx+c,當x=0時,y=c,所以拋物線與y軸的交點坐標是(0,c),由此可以得出如下結論:c>0時,拋物線與y軸正半軸相交,反之也成立;c<0時,拋物線與y軸負半軸相交,反之也成立。所以,c號通常是根據拋物線與y軸正、負半軸的相交情況確定。
根據前面的分析,現在咱們大致了解了a、b、c三個字母號的判斷:根據拋物線開口方向判斷a號;根據對稱軸號來判斷b號;根據拋物線與y軸哪個半軸相交來判斷c號。
接下來講解如何判斷a、b、c組合出來的代數式號。
如何判斷a+b+c號:
對于二次函數y=ax²+bx+c,當x=1時,函數值y=a+b+c,所以只需判斷x=1時的函數值號,就是a+b+c號。
同理,只需判斷x=-1時號,就是a-b+c號;只需判斷x=2時號,就是4a+2b+c號;等等。
不知道你聽懂了沒有?沒太懂也沒關系,結合下面這2道例題,你就能做到清清楚楚,明明白白。
例1
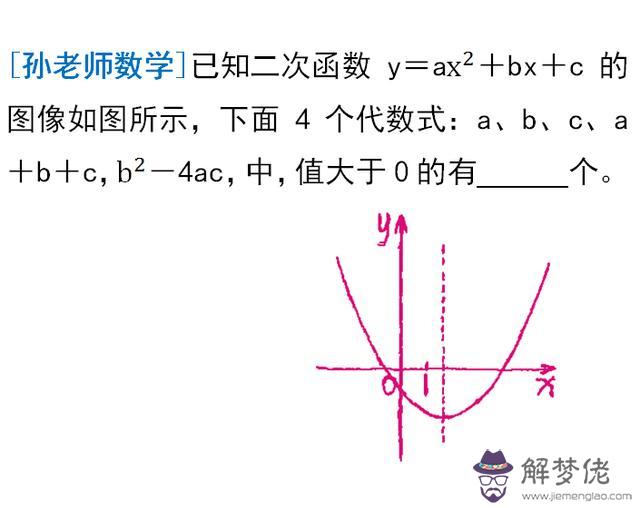
請結合上面所講,弄明白下面的解析過程。

例如,判斷a+b+c的詳細過程:根據題中的示意圖可知,當x=1時,二次函數的圖像在x軸,即對應的函數值為負數,把x=1代入二次函數的表達式y=ax²+bx+c中可得函數值y=a+b+c,所以a+b+c是負數。
例2
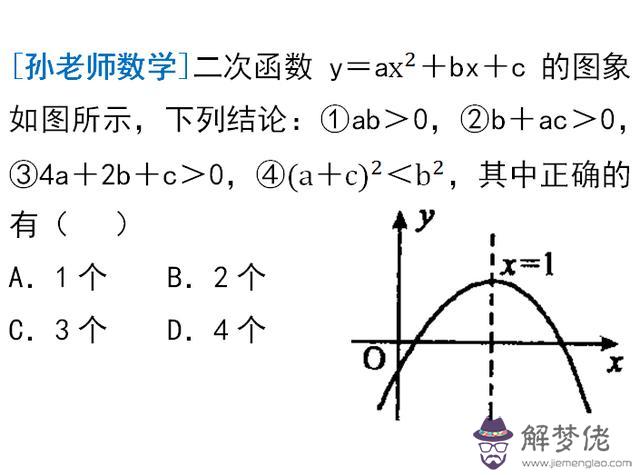
先通過確定a、b、c號,判斷①和②的對錯,過程如下。

判斷③4a+2b+c>0的對錯:
如下圖,根據拋物線的對稱性可知:BM=AM<1,所以OB=1+BM<2,所以2在點B的右側,所以當x=2時,函數值y是負數,把x=2代入y=ax²+bx+c得函數值y=4a+2b+c,所以4a+2b+c<0;故③錯。
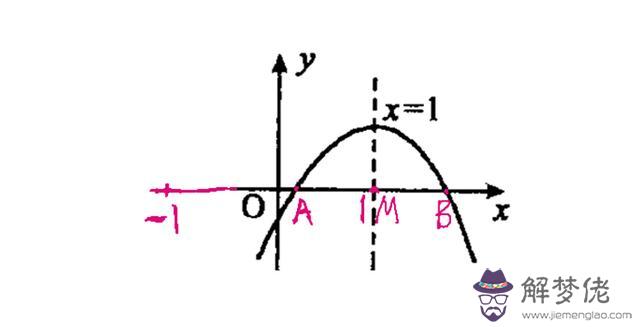
判斷④的對錯:
如上圖,當x=1時,函數值y>0,即a+b+c>0;當x=-1時,函數值y<0,即a-b+c<0;所以:

加油!
以上就是與怎樣判斷函數開口向上還是向下相關內容,是關于拋物線的分享。看完a0開口向上還是向下后,希望這對大家有所幫助!
本文來自:解夢佬,原地址:https://www.jiemenglao.com/suanming/389105.html

















