初中數學,幾何證明輔助線技巧方法。通過這些類型,基本可以學會包括初中輔助線大多數技巧方法。所有題目都是作者自己選題,自己畫圖,而且每道題都有視頻講解。
1、平移法,當一個圖形有兩條相等線段相交,其夾角為特殊角時,一般都是平移。或者兩條關聯線段需要轉化通用三角形時,也可以用平移法。初中范圍內關于這類題不是很多,大約掌握十題左右就差不多了。分類刷題,總結方法,舉一反三,學習努力很重要,但怎麼學更加重要。
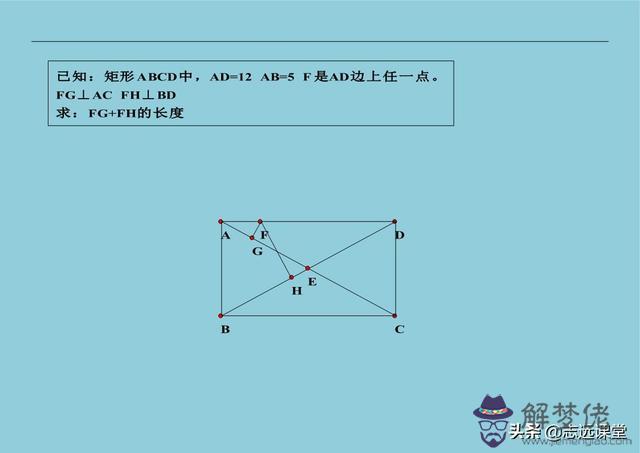
2、面積法解題,一般這樣的題的特征都是兩個以上的直角。可以用面積法找到等量關系,也稱為等積法。這樣的題在初中范圍內出現的不多,典型的也就不超過十題,而且還是互相變化得到的。所以只要掌握很少的幾題,這類面積問題就可以過關了。下面給出的是比較典型的模型常考題,同學們可以參考一下。
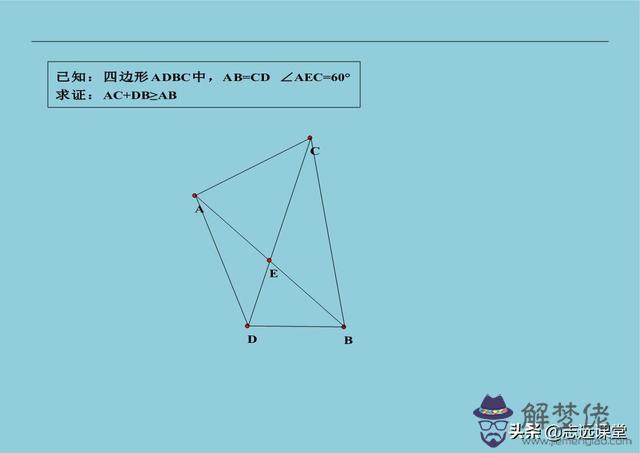
3、八字證明線段大小關系,大家都知道八字倒角法,其實八字還有一個結論就是線段大小關系。結論就是交叉兩條線段之和大于另外兩條線段之和。所依靠的知識點是,三角形兩邊之和大于第三邊,有了這樣的提示此結論不難證明。然后運用此結論解決下面這道例題,我們平時做題不要為了完成答案而做題,更應該去想這一類題的特征以及解決方法。
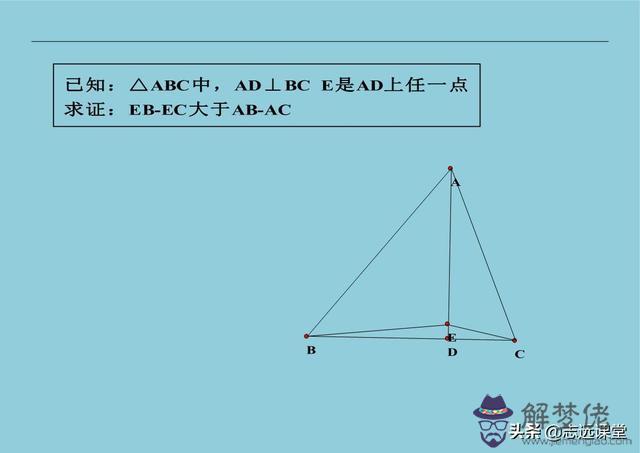
4、四邊形中點輔助線,遇到有四邊形(平行四邊形、矩形、菱形、正方形)有邊中點。一般都是中點處的線段進行延長,可以得到八字全等圖形。因為平行和中點組合,就是構造八字全等圖形的特征。下面的習題大家可以按照這個解題思路試一下,以后遇到類似已知就能做到舉一反三的效果。
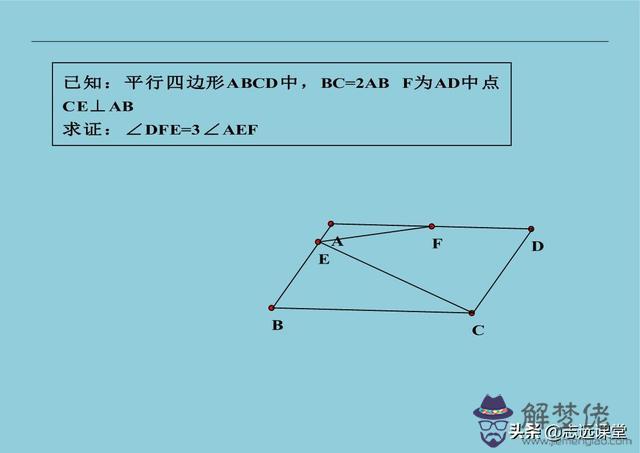
5、手拉手模型(也叫子母圖、哥倆好、初中第一圖、神圖等),兩個一大一小兩個相似圖形共頂點。常見的是兩個等邊三角形、兩個等腰直角三角形、兩個正方形等。這個圖形常見結論就是出全等,而由全等可以擴展出十幾個其它結論,大約一年前我曾經發過這十幾個結論。而且這個圖形還和其它一些模型有聯系,比如費馬點、托勒密定理等。由此基本圖形擴展出的中考題不計其數,記得十年前,我教過的一位同學,把這個圖和結論掛在墻上。同時幸運的是,那一年中考就是手拉手的變形,哪個時候還沒有出現手拉手這個名字,我稱這個模型叫初中第一圖,現在某網站上還有我錄的視頻講解。可是現在,十年過去了,這個模型已經被玩壞了,被老師們研究的太透徹,好多省市已經不敢考這個圖形了。
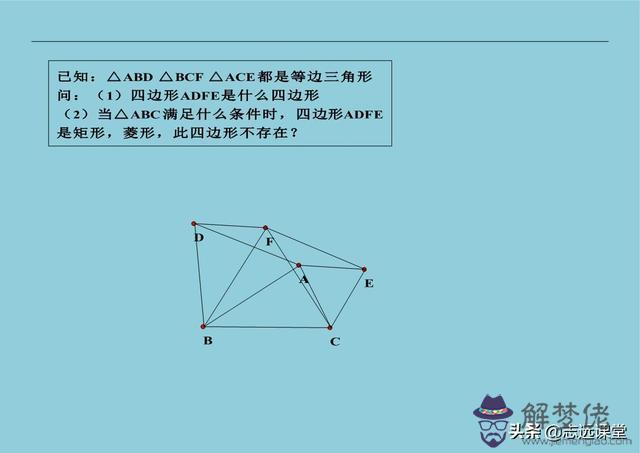
6、等腰三角形(包括等邊)常用輔助線。做三線合一; 做一邊的平行線,出小等腰; 延長一腰至等長,連接后出直角三角形; 等腰外面擴等邊,連接兩頂點出30度角。
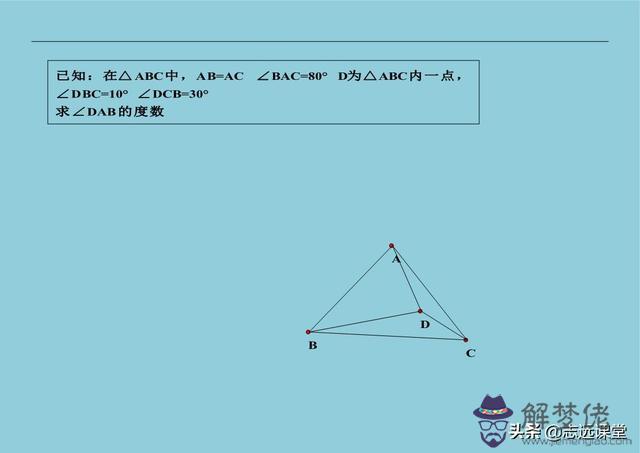
7、等腰直角三角形常用輔助線,兩直角邊處構造全等。因為等腰直角三角形有相等的邊,而直角又很容易為全等角相等創造條件,而且等邊三角形和正方形有時候也符合這個規律。這個方法出自教材中的“趙爽弦圖”,無論是三垂直模型,還是其它類似問題。
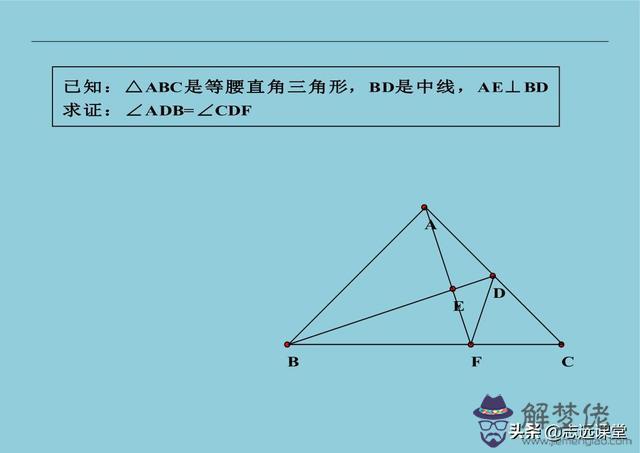
8、初中有一種不常考的類型,藏角題。一般這類題都是利用線段之間的數量關系,產生特殊角度。沒刷過這類問題的同學,確實有一定難度。大家可以參考下面習題,研究一下這類問題,注意不是會做就可以了,而是探索這類題的特征與方法。特別是教學人員,會做題只是教學的初級層次,研究教法、教會不同層次的學生才是重要的,別跑偏了!
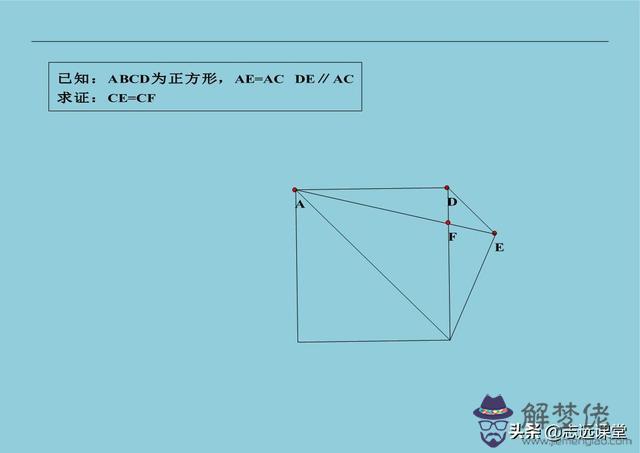
9、旋轉輔助線特征:已知中有相等的線段共頂點; 對角之和180°; 半角模型是旋轉; 費馬點是旋轉; 手拉手(哥倆好、子母圖、初中第一圖)模型是旋轉,還有其他特征可供學習。
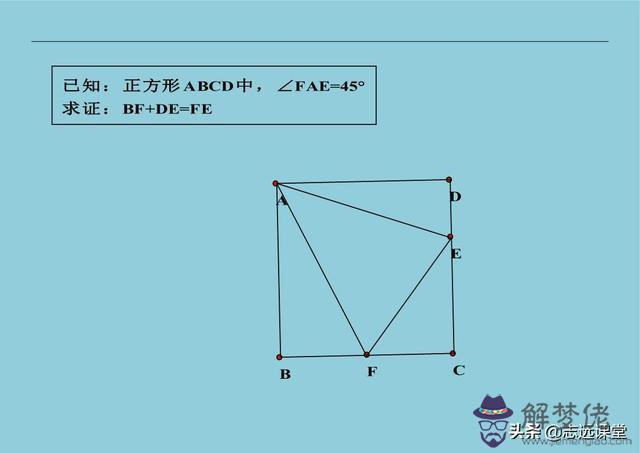
10、直角三角形中點輔助線:有斜邊中點連斜邊中線; 有斜邊倍分關系時,做斜邊中線或延長至等長。 就上面兩句輔助線總結,無論學生還是老師,都有參考價值。
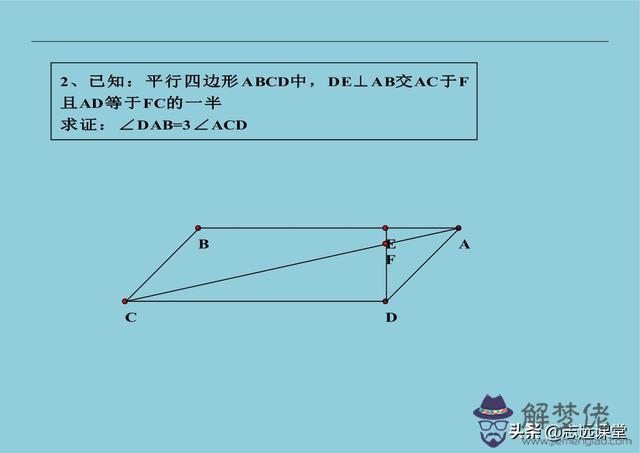
11、角平分線截取證全等:已知中有角平分線,在長邊上截取線段等于短邊,截取的點與角平分線上某一點相連,出全等。當然,如果延長也可以,這就是老師常說的截長補短。這才是真正的教方法技巧,簡單直接,一看就懂!
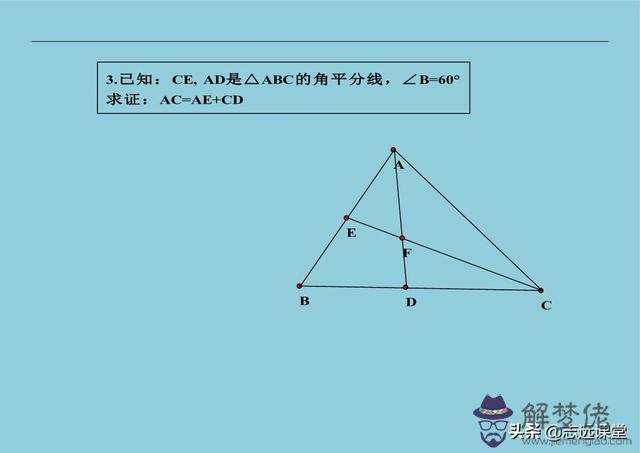
12、角平分線延長出全等:已知中被平分的角一邊上有一點,向角平分線有垂直線段,一般都是延長與另一邊或其延長線相交,出全等。看懂這句話,你就又學會了一種輔助線做法,價值比上一次一對一都要高,用這種方法,解決一下下面的習題吧!
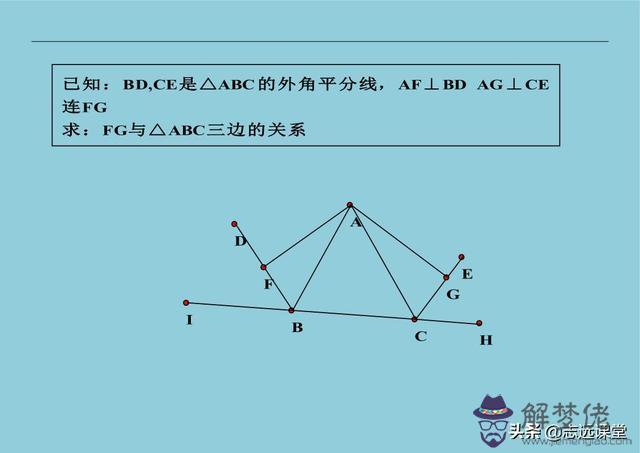
13、已知中出現兩個中點:一般都是在某邊上再找一中點,與已知兩中點相連,構造兩個中位線。這是比較常用的輔助線技巧方法,仔細體會一下吧!用這麼少的語言告訴您方法,一定是干貨。
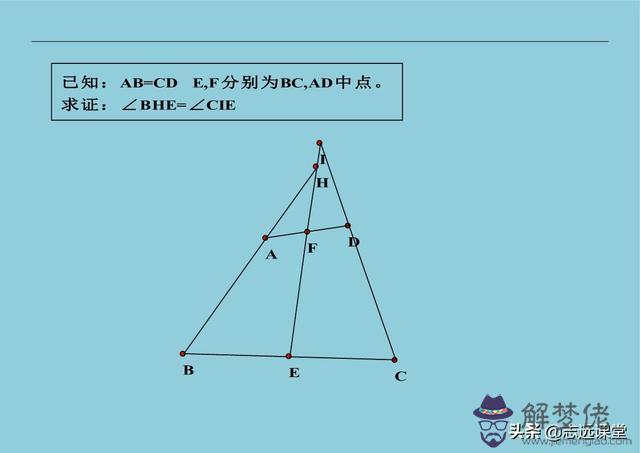
14、一個中點如何做輔助線,構造八字全等。一般都是倍長相等的線段,出現全等三角形,而且還有平行的線段。
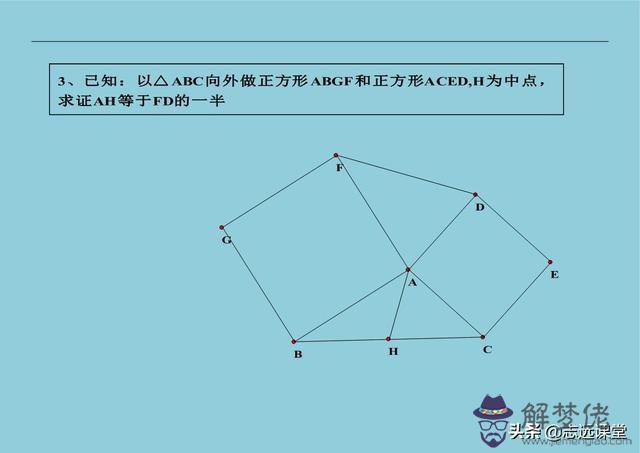
上面所總結的,是初中數學幾何輔助線文字記憶版。所有方法為志遠老師總結,此文章可以不作為商業用途,隨意使用。
本文來自:解夢佬,原地址:https://www.jiemenglao.com/suanming/380030.html

















