
作者 | 李夢樵
來源 | 《中學數學教學》1983年02期
二、《九章算術》
《九章算術》成書于何時已不可考。三國時魏劉徽為《九章算術》作注。序言中有以下一段:“按周公制禮,而有九數,九數之流,則九章是矣。往者暴秦焚書,經術散壞,自時厥后,漢北平侯張蒼(公元前250年—前152年,河南陽武縣人。在秦為御史,漢高祖六年封為北平侯,漢文帝時為丞相歷十五年,享年百余歲),大司農中丞耿壽昌(公元前73年—前49年),皆以善算命世。蒼等因舊文之遺殘,各稱刪補,故較其目,則與古或異,而所論者多近語也。” 由此可見,《九章算術》在西周初期已具雛形,以后有所修訂補充。張蒼、耿壽昌兩次刪補,更換篇目,并把古人的敘述換成漢代語言,使《九章算術》成為定本。
據傳古代九章中有“重差”、“夕桀”、“旁要(音腰)”而沒有“勾股”。重差術有劉徽專著,即《海島算經》。旁要、夕桀世無傳本。據清代學者研究,“旁”即“邊”,“要”同“腰” ,“旁要”即研究圓的內接形和外切形;“夕”有“斜”的意義,“桀”古同“磔”,有分裂的意義,“夕桀”當系研究中線、角平分線、高線。由于這些線把三角形分成兩部分,古人重視面積,故名夕桀。旁要、夕桀的失傳,可能是毀于秦火,也可能是張、耿等人從古九章刪去,而“方程”與“勾股”,可能是張、耿等人所加。因“方田”章即有“方程”,“商功”章即寓“勾股”也。
《九章算術》在明代失傳。清乾隆時修《四庫全書》,戴震等從《永樂大典》中輯出。《大典》所載沒有圖形,戴震為之補繪。現存《九章算術》,即戴震所輯出之本,有魏劉微與唐李淳風注釋。另有李潢(乾隆36年進士)著《九章算術細草圖說》九卷,附《海島算經》一卷。
《九章算術》分方田、粟米、衰(音崔)分、少廣、商功、均輸、盈不足、方程、勾股九章,共有246個問題。各章內容摘要敘述如下。
第一章“方田”共38問。主要講計算田畝面積的方法,有方田(正方形)、直田(矩形)、圭田(三角形)、邪田(梯形)、圓田(圓形)、環田(環形)、弧田(弓形)等等。其中方田、直田、圭田、邪田的公式是正確的,圓田、環田、弧田,古法用π=3是粗糙的,弧田的公式并不正確,竟然沿用了二千年之久。劉徽在這里指出,“徑一周三”是內接正六邊形的周長,應該小于圓周,他用割圓法提出π=3.14,后人把3.14叫做徽率。注中又有π=3.1416,清代李潢認為是祖沖之的創造,近代數學家錢寶琮、華羅庚、錢偉長、歷乃驥以及日本三上義夫均認為劉徽所創造,劉徽既發明割圓術,創造π等于3.1416只是一舉手之勞。
這一章中,還講到分數運算法則,在約分術中,講了用輾轉相除法求分子、分母的公約數。
第二章“栗米”共46問。大部分講糧食交換的計算。先規定交換率,用“今有術”(即比例,歐洲叫做三數法則)進行計算。這一章還用到很復雜的復名數化、聚的方法。
第三章“衰分”共20問,是講配分比例和等差、等比數列等問題。
第四章“少廣”共24問,講平面的面積和球的體積。講了開平方、開立方的計算。還有已知球的體積求直徑的方法。
第五章“商功”共28問:是講立體的體積計算,其中名詞,今多已不用。這里用公式表示書中敘述的各種立體的體積的計算方法。
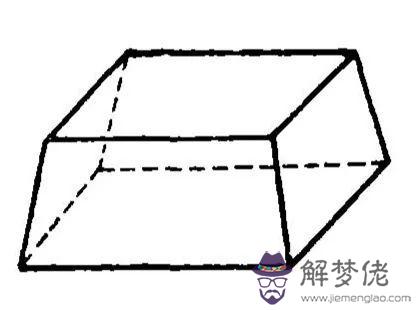
城、垣、堤、溝、塹、渠都是一種平截頭楔形,上下底皆是矩形。上底寬a長c,下底寬b長c,體積V=(a+b)ch。
“倉”是長方體;方堡壔(音島)是上下底都是正方形的柱體,圓堡壔是直圓柱,方亭是上下底都是正方形的棱臺,圓亭是圓臺,方錐是底面為正方形的棱錐,還有圓錐。
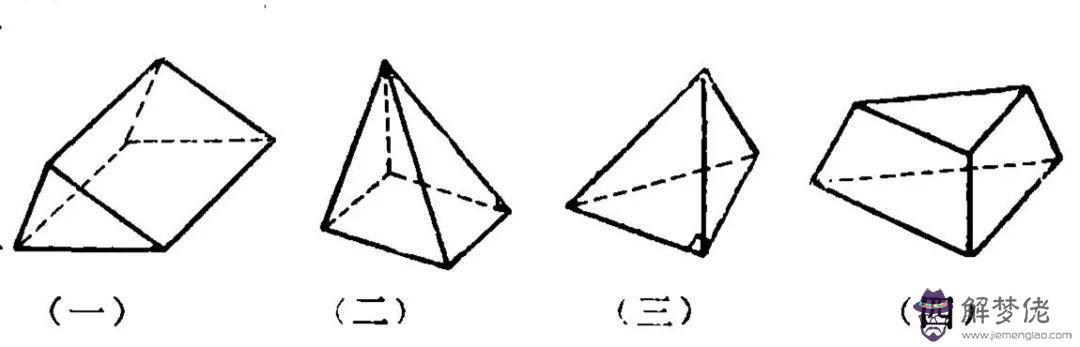
塹堵:一矩形柱體依對角面剖開(下圖一)
V=abh
陽馬:底面為長方形而有一棱與底面垂直的錐體(下圖二)
鱉臑(音鬧):底面為直角三角形而有一棱與底面垂直的錐體(下圖三)
方亭:圓亭:
羨除:楔形體的三個側面不是長方形而是梯形(下圖四)
這個公式歐洲認為是勒讓德(Legendre,1752—1833)發現的,比中國晚了二千年。
芻甍是形如草房頂的楔
芻童、曲池、盤池、冥谷都是長方臺
這些公式都是正確的。最有趣的是芻童公式改寫為:
V=h(2ab+ad+2cd+bc)=h[ab+cd+(ab+ad +cd+bc))=h[ab+cd+(a+c)(b+d)]=h[ab+cd+4×(a+c)×(b+d)]
此處ab是上底面積,命為,cd是下底面積,命為,(a+c)×(b+d)是中截面面積,命為。得V=h與擬柱體的體積公式相同。
第六章“均輸”共28問。是大統一時代,處理國民平均負擔的問題。李約瑟說,歐洲研究這些問題要晚得多。
《九章算術》均輸章的第一個問題:今有均輸粟,甲縣一萬戶行道8日,乙縣9500戶行道10日,丙縣12350戶行道13日,丁縣12200戶行道20日,各到輸所,凡四縣賦當輸25萬斛,用車一萬乘。欲以道里遠近、戶數多少衰出之,問粟、車各幾何?
解:100008 =1250, 950010=950, 1235013=950, 1220020=610,
甲:乙:丙:丁=1250:950:950:610=125:95:95:61
而125 + 95 + 95 +61 =376
(甲)
(乙、丙)
(丁)
由于車數須為整數,用四舍五入法得甲縣出車3324乘,乙、丙兩縣各出車2527乘,丁縣出車1622乘,2500001000=25(斛),甲縣出粟3324×25=83100(斛),乙、丙兩縣各出菜2527×25=63175(斛),丁縣出粟1622×25=40550(斛),李約瑟認為這類問題歐洲很少人提到,至公元8世紀,才在數學難題中出現。
第七章,“盈不足”共20問。是我國古代解決問題的一種巧妙的方法。除盈不足、兩盈、兩不足等問題外,還用來解某些等比數列問題。如第十一問。
今有蒲生一日長三尺,莞(音管)生一日長一尺,蒲生日自半,莞生日自倍,問幾何日而長等。
原解:設為2日,蒲生3+1.5=4.5(尺),莞生1+2=3(尺),4.5-3=1.5(尺)(不足)。
設為3日:蒲生3+1.5+0.75=5.25(尺),莞生1+2+4=7(尺),7-5.25=1.75(尺)(盈)。
1.75×2+1.5×3=3.5+4.5=8, 8(1.75+1.5)=83.25=2(日),蒲長3+1.5+0.75×=4.5+=4(尺),莞長1+2+4×= 413(尺)。
今解:設所求日數為n,有即,
,即, =1則n=0不合,=6則n==2.5849(日),蒲長=5。莞同。
“今解”與“原解”不一致,是因為“原解”把每日生長率看成勻速,而“今解”把每日生長率看成變速。
第八章“方程”共18問,主要講一次方程組的解法,未知數多達五個。“方”是把一個算題排列成方陣的形式,“程”的古義是度量、程式。
這一章最寶貴的遺產是在全世界上首先突破正數的范圍,提出負數,并提出“正負術”(正負數加減運算法則)。劉徽在注中說,正數用赤籌,負數用黑籌,或將籌斜放(負)和正放(正)來區別。以第八問為例。
今有賣牛二、羊五以買十三豕,有余錢一千,賣牛三、豕三以買九羊,錢適足,賣羊六,豕八以買五牛,錢不足六百,問牛羊豕各買幾何?
書中“術日” (解法),用現在的方程寫出來就是下面三個方程:
2x+5y-13z=1000, 3x-9y+3z=0, -5x+6y+8z=-600。
方程章第13問是不定方程。譯成今文如下:今有五家共井。若用甲家繩2條吊水,缺少的正好是乙家繩1條,用乙家繩三條,缺少的正好是丙家繩一條,用丙家繩4條,缺少的正好是丁家繩一條,用丁家繩5條,缺少的正好是戊家繩一條,用戊家繩6條,缺少的正好是甲家繩一條,如果各家都能得到缺少的一條。都正好吊著水。問井深和五家的繩長各若干?
設甲、乙、丙、丁、戊五家的繩長各為x、y、z、t、u丈,井深為w丈。
則有 2x+y=3y+z=4z+t=5t+u=6u+x=w
得x:y:z:t:u:w=265:191:148:129:76:721。
書中用這些數(如265是2丈6尺5寸)作為答案,可能是根據具體情況,一般井深不超過10丈也不少于4丈。
第九章“勾股”共24問。用勾股定理解答實際問題。例如第六問:“今有池方一丈,葭生其中央,出水一尺。引葭赴岸,適與岸齊。問水深、葭長各幾何?”
又如第九問:“今有圓材埋在壁中,不知大小。以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?” (徑指直徑)解法中用到“垂直于直徑的半弦的平方等于直徑被弦所分兩段乘積”這一性質。
第十五、十六兩問是“勾股容方”、“勾股容圓”問題。就是求直角三角形的內接正方形邊長和內切圓直徑問題。
還有一些問題,要用到一元二次方程。這里不一一列舉。
《九章算術》不僅內容豐富,影響也深遠。元朱世杰的《四元玉鑒》和明程大位的《算法統宗》都有類似于勾股章的第六問。“今有方池一所,每邊丈二無疑。中間蒲長一根肥,二尺水面高起。斜引蒲稍至岸,恰與水面相齊,知君明算并無欺,蒲長水深各幾?”后來傳到印度。在印度作家書中有:“平平湖水清可鑒,面上半尺生紅蓮,出泥不染亭亭立,忽被強風吹一邊。漁人觀看忙向前,花離原位二尺遠。能算諸君請解題,湖水如何知深淺?”(引自《趣味幾何學》第69頁)

本文來自:解夢佬,原地址:https://www.jiemenglao.com/suanming/364616.html

















