伏羲的一,就是古代數理大一統文化概念中的這個一統這個詞里的一。它并不僅僅是數學的一。它是一種包括全部的古代數理文化方式的表達。
如果以一分為二的分形方式向下分形,就是陰陽兩儀,之后兩儀生四象,四象生八卦。這是世界數學史乃至世界人文史上最早的分形觀念的明確表達,筆者想不出更簡單的分形數學規則了。
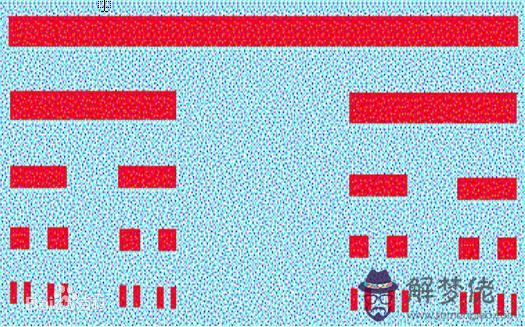
三分康托集
上圖,這是數學的三分康托集,千萬不要以為筆者在畫八卦,這在好好地說數學。
1883年,德國數學家康托(G.Cantor)提出了三分康托集,或稱康托爾集。被西方認為這是現代分形數學研究的“開端”。
先談一下當時的歷史文化交流的背景。從18世紀末黑格爾對孔子偏頗的哲學批評中可以看出,當時西方或者說德國已經了解中國古代的哲學思想,包括儒學。后來,《道德經》在德國,成為發行量僅次于希特勒的《我的奮斗》一本書。也就是在十九世紀,系統性的中國傳統文化已經在走向西方。
而二十世紀初期,地球村的熱點在德國,兩次世界大戰與其有關。經濟方面,當時德國的鋼鐵產量世界第一;文化方面,誕生了馬克思等哲學家、思想家;物理方面,愛因斯坦的原國籍是德國。二戰后,美國接手了德國的科研資料和大部分科學家。
從三分康托集可以看出,康托受到了伏羲八卦的啟發。當然,他在繼承伏羲數學思想的前提下,進行了進一步的加工。他使用的數學規律就是太極生兩儀,或者說一分為二。但是他把陰爻用兩個1/3的線段來表達,這很有創意的。
伏羲并沒有說陰爻該如何準確畫。以至于后世,也有把陰爻畫成折線的、曲線的,馬王堆出土的卦象圖符就是用折線表達陰爻,和我們通常看到的陰爻并不同。然而,正因為伏羲沒有準確說,所以陰爻的縫就成了量子化的數理文化概念。
陰爻的這個縫可以看見,存在。但是陰爻的兩個線段只有都是0.5,才能和陽爻的1相等。而陰爻兩個線段明顯看見的不是0.5的長度。那麼,這個看到的陰爻的縫到底是有還是沒有呢?這是個數學問題。
這也是現代量子理論的基礎問題。薛定諤的那只貓,到底是活的,還是死的。決定權在觀察者。陰爻的這縫是有還是沒有呢?與觀察者有關。這學問就大了。

伏羲量子二分集-分形數學的鼻祖-你可和三分康托集比較一下
甲骨文的啟發—伏羲先天八卦的量子化表達—先從“一”說起
甲骨文的啟發—伏羲八卦中的量子化表達—先從“一”說起(二)
(注:《國學溯源之旅—分形數學理論在中國應該稱為伏羲分形理論更準確些》(2018-05-11)在頭條上連載這一篇的時候,筆者還不是頭條的原創作者,因此不能鏈接,請自行在筆者文章中查找。)
“1975年,Mandelbrot“創立了”分形幾何學(Fractal Geometry)。在此基礎上,形成了研究分形性質及其應用的科學,稱為分形理論。”
古代東方、西方都沒有現代數學意義的分形這個詞,這個詞是Fractal -原意是不規則碎片形,分形是現代的意譯和衍生。上世紀七十年代,西方據說是“發明了”分形和分形維數學,然后就被翻譯過來,我們才知道分形在西式數學里是個什麼東西。
在中國古代,使用的是循環這個數理兼容的表達方法來兼容表達出來現代數學分形的這個概念,而分形僅僅是循環這種古代數理表達兼容的數學內容之一。
這三分康托集不是八卦,你真的敢肯定?

疑惑
那麼一系列的小問題產生了。分形這個概念是誰發明的?什麼時候產生的呢?原產地在哪里?西方是發明了、創造了分形數學,還是發展了分形數學?
基于八卦兼容的這種類似數學二進制表達的啟發,西方還產生了摩爾斯電碼,還導致了二進制計算機的產生。都是利用這麼一個最簡單的一分為二的分形數學原理的引申。
西方有些人,無論在寫世界數學史還是世界歷史的時候,總是把中國這麼一塊地方“不小心地”就給忘卻了。所以,西方的世界數學史通常沒有包括中國的數學史,而一些人看的中國數學史又是西方人寫的,這誤會就大了。
中國古代,無論八卦、64卦、五行、太極,都是具有分形數理觀念的表達。那麼,分形,誰發現的?
當然,筆者可能忘了一件事情,中國人看這幾種古代的數理模型,又有多少人看出有分形數學概念的?那就不說外國人了。
說的這麼熱鬧,別問筆者“分形是什麼?”這種基礎的問題,自己看數學書吧。
如果我們自己寫數學歷史,說清楚一些,這個總比看西方人寫的中國數學史把握一些。

周脾算經
圓與方,直與曲,在古代數理文化中是兼容一體的表達,數學對此表示強烈不滿鑒于天圓地方這個最古老的數理一統方案,也就是河圖、洛書基于中間的五形成的古代數理文化的一統方案,也就是伏羲說的一。
這個一,人文上或者說對于古代數理文化而言,可以是孔子說的直線,如山,如《連山》。也可以是老子說的曲線、波動,如水,如《歸藏》。這是一對陰陽;當然,也可以是老子的圓,文王的方,這又是一對陰陽;后來,這成了歷史上兩個主要的數理文化發展方向。
為何中國古人不管信道教還是信儒學的,都尊伏羲為人文始祖,原因就在這里。直與曲,方與圓數理文化表達說的都是一樣的事情,伏羲的一。解讀的出發點相同,使用的具體數理解讀方法不同而已。
這種一而二,二而一的思維方式,實際也是西方現代的數理文化分化的方式。
笛卡爾基于前提數學條件,利用坐標系統一了分道揚鑣近2000年的代數、幾何表達。但是,他繞過了古代最頭疼的數理文化中數的一個重大問題--直線與曲線的兼容表達。這在數學上是不可能完成的任務,只能無限逼近,不能相等。而中國古代數理文化,輕易地用數理文化的方式解決了這個數學最頭疼的事情。
祖沖之當時還是沿著現代數學的發展主線在走,用多邊形切割圓的方式,計算了圓周率的密率。這種數學思維方法,后來衍生出數學的窮舉法、無限逼近、微積分等概念。也就是當時的數理文化就知道數學這個問題,不過,并未數學性地在意,采取了夠用就行了的實用態度,小數點后面弄那麼多位,實用性意義太小了。
而西方數學,沿著這個思路繼續走了下去,1000多年后,牛頓產生了微積分數學,同期,中國清朝的一位蒙古人也正在研究微積分。
再后來,愛因斯坦的相對論、物理的基本粒子領域繼承的是周易的直、方、實為基礎的發展方向,用直觀察表達曲,用實表達虛;而特斯拉、量子理論、弦理論,這繼承的是老子的曲、波、虛的發展方向。用曲觀察表達直,用虛表達實。這樣表達,數學的繼承發展的脈絡也就清楚了。
而混沌和分形維,這是在直與曲之間的特性,也就是即陰即陽、或陰或陽的一種兼容狀態。這中國古人也研究了。分形的問題,伏羲開頭研究,后來周易、五行、太極都數理表達了。至于混沌數學的蝴蝶效應,這個偏向于用曲表達方便一些,太極圖也就給數理表達了。
太極圖中的混沌數學以及太極圖與《周易》元亨利貞四階段的兼容
你可能從未想過的問題,“太極生兩儀”為什麼
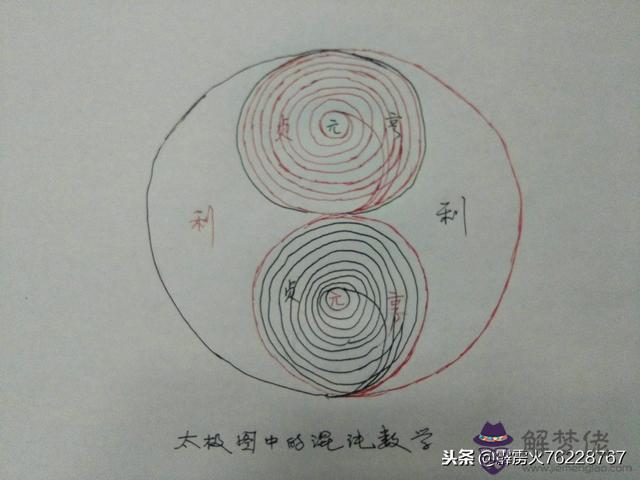
太極圖表達的混沌數學中的蝴蝶效應圖
基于伏羲的一產生的直與曲的兩種數學分化,量子理論和相對論不能協調一統,這事是必然的。西方物理的瓶頸也就在這里。中國就沒這文化問題,都是伏羲的一的事情,做事就夠了。
有些崇洋的人一見到這類文章就留言聲討,說這是愣給古人臉上貼金,筆者就想問兩句,“西方的數學你懂嗎?中國古人的數理你真懂了?”都不懂,那只能拉黑處理,頭條這拉黑功能真是不錯,避免擾民。
先人用《周易》數理中的數算出“第十大行星”,還敢稱懂周易的,不妨試試算一算有人至今還不懂1772年提出的提丟斯–波德定律 R=0.3×2^n-2+0.4,這就是一個單邊拋物線的數學擬合方法,這種數學擬合到了海王星就出現大幅偏差,因為波德不懂相對論的曲率變化嘛。
《甲骨文的啟發—數學上方圓可否一統?—提丟斯-彼得是數理殘余!》(2018-04-16,筆者較早文章,不能鏈接,請自行搜索筆者頭條文章。)
這種相對粗略的線性數學擬合,即便用西方古代的輪中輪這種數學工具,模擬的誤差比這種方法要小很多,就是有些復雜。用周易方式模擬,也比這種方法也要精確的多。

輪中輪擬合太陽系軌道
2005年,美國的麥克布朗利用望遠鏡發現了號稱的太陽系的第十大行星,當然這是一個誤會,現在該行星被稱為鬩神星,與冥王星一起歸為矮行星。實際上,即然有小行星帶這種命名方式,那麼冥王星、鬩神星這區域,完全可以命名為冥王星帶,該軌道區域與小行星帶存在明顯的分形擬合相似的數學規律。外國天文學的這種行星命名方式,有時候很蹊蹺,都是西方神話故事里面的人物,且受古代西方數理文化影響。
實際上,早在65年前,一位中國人劉子華運用《易經》的方法就已經推算出該行星的位置,他稱為木王星。他的論文被西方公示、發表,并提出密度、速度、距離、周期參數。當然,驗證發現有些誤差。
他相當于用八進制的數學方法,擬合了太陽系的行星數據,從而推算出來這個第十大行星。(詳情請參考頭條Allhistory的文章,《縱橫全歷史,“東方哥白尼”轟動歐洲,竟因為用易經研究太陽系》)

一些并不懂易經數學原理的中國人,對此大加批判。實際上,我們習慣了數學的十進制,這種方法對于數學而言是簡便的,但是中國古人數理用的是兼容進制表達。當你把八卦確定為八進制使用的時候,它就是八進制數學的基礎。
我們天天用的電腦,說是二進制的,實際為了簡算,內核使用的是十六進制。為什麼會有1kb=1024b,而不是1000b的數學原因就在于,64*16=1024。這也是周易的數學原理。這些不懂易經數學原理的中國人,抽空把電腦也批一批,就更顯得智商爆表了。對于不懂的東西,批的是什麼?
提丟斯–波德定律這個數學擬合方法至海王星已然失效,易經計算邏輯方式到了鬩神星有誤差。還敢稱懂周易的,不妨也試試算一算。
順便數學性地提醒一下:在擬合數學線性規律未發生改變的時候,擬合規律有預測作用。如果規律發生改變,或者遇到隨機、混沌體系,那麼這個規律毫無數學擬合唯一性的預測意義。也就是用線性數學方法解決非線性的問題容易出數學問題;反之,亦然。
這就是伏羲的一里面包含的直與曲的數學問題。古人的解決之道是數理兼容,這時候不跟你談數學了,講人文。
今天談的是“一劃分陰陽”這個數理的數學發展方向,明天說說伏羲的“一畫開天地”這個人文發展方向。
待續。。。。。。
本文來自:解夢佬,原地址:https://www.jiemenglao.com/suanming/360954.html

















