本文轉自數學縱貫線公眾號。
本文作者林開亮,任教于西北農林科技大學理學院。
關注微信:哆嗒數學網 每天獲得更多數學趣文
新浪微博:http://weibo.com/duodaa
上集
我第一次去城里,是在很小的時候——20多年了,也許是小學五六年級,跟著一個種菜的表姑媽推著板車去常德縣城蔬菜市場賣菜。我當時一定頭一次吃到不少好吃的,但現在想不起來了,不過我還記得當時我拆了一個算命先生的臺,為此我表姑媽頗為得意。這種猜姓氏的把戲估計大家都見過,以下是我當時遇到的版本。
首先算命先生會攤開一張百家姓的大圖紙,里頭有很多小格子,每個小格子里有一定數目的姓氏,大圖紙旁邊會放一些小紙片,每張小紙片上會有一定數目的姓氏。他會要求你用有你姓氏的小紙片蓋住大圖紙上那個有你姓氏的格子,然后他“掐指一算”,就報出了你的姓氏。我見識過幾次,沒有不準的,來算命的無不稱奇慨嘆!我也好奇他是怎麼做到的,后來我想明白了,一定是小紙片和蓋住的小格子上只有一個相同的姓氏。我拿起小紙片一對照,果不其然。后來,我也開始賣弄了,只要有人用小紙片蓋好小格子,我就拿起來迅速一對照,結果有幾次比算命先生還先得出結果,我記得當時猜中一人姓蔣(與委員長同姓,所以印象深刻)。他老人家臉上開始不好看了,于是就喝令我一邊玩去。
20多年過去,大街上仍然有算命先生玩這個把戲,仍有不少人疑惑不解,乃至迷信其神。網上有不少朋友追問這個把戲究竟什麼玄機,也有人解密,不過他們似乎沒有真正講明白這一點——如何保證小紙片和蓋住的小格子上只有一個相同的姓氏?例如,見2017年春節期間的一個視頻。

這里我想介紹一個思路(最近偶然想到,算命先生也許用別的,但我想絕不至于比這方法還簡單了),它也許是最簡單的,可以保證每個人都能當一回“神算子”。
首先,我們要有一張大圖紙,上面分布著常見的百家姓。按照百度百科,
《百家姓》,是一篇關于中文姓氏的文章。按文獻記載,成文于北宋初。原收集姓氏 411個,后增補到568個。為簡單起見,我們這里僅選取出現頻率最高的前300個姓氏,以下排名取自網絡(排序是否準確與猜姓氏無關,要緊的是,我們只需要給出一個排序)。
2017年中國人口最多的前300大姓1:李2:王3:張4:劉5:陳6:楊7:趙8:黃9:周10:吳11:徐12:孫13:胡14:朱15:高16:林17:何18:郭19:馬20:羅21:梁22:宋23:鄭24:謝25:韓26:唐27:馮28:于29:董30:蕭31:程32:曹33:袁34:鄧35:許36:傅37:沈38:曾39:彭40:呂41:蘇42:盧43:蔣44:蔡45:賈46:丁47:魏48:薛49:葉50:閻51:余52:潘53:杜54:戴55:夏56:鐘57:汪58:田59:任60:姜61:范62:方63:石64:姚65:譚66:廖67:鄒68:熊69:金70:陸71:郝72:孔73:白74:崔75:康76:毛77:邱78:秦79:江80:史81:顧82:侯83:邵84:孟85:龍86:萬87:段88:漕89:錢90:湯91:尹92:黎93:易94:常95:武96:喬97:賀98:賴99:龔100:文
2017年中國人口最多的前100至200大姓101:龐102:樊103:蘭104:殷105:施106:陶107:洪108:翟109:安110:顏111:倪112:嚴113:牛114:溫115:蘆116:季117:俞118:章119:魯120:葛121:伍122:韋123:申124:尤125:畢126:聶127:叢128:焦129:向130:柳131:邢132:路133:岳134:齊135:沿136:梅137:莫138:莊139:辛140:管141:祝142:左143:涂144:谷145:祁146:時147:舒148:耿149:牟150:卜151:路152:詹153:關154:苗155:凌156:費157:紀158:靳159:盛160:童161:歐162:甄163:項164:曲165:成166:游167:陽168:裴169:席170:衛171:查172:屈173:鮑174:位175:覃176:霍177:翁178:隋179:植180:甘181:景182:薄183:單184:包185:司186:柏187:寧188:柯189:阮190:桂191:閔192:歐陽193:解194:強195:柴196:華197:車198:冉199:房200:邊
2017年中國人口最多的前200至300大姓201:辜202:吉203:饒204:刁205:瞿206:戚207:丘208:古209:米210:池211:滕212:晉213:苑214:鄔215:臧216:暢217:宮218:來219:嵺220:茍221:全222:褚223:廉224:簡225:婁226:蓋227:符228:奚229:木230:穆231:黨232:燕233:郎234:邸235:冀236:談237:姬238:屠239:連240:郜241:晏242:欒243:郁244:商245:蒙246:計247:喻248:揭249:竇250:遲251:宇252:敖253:糜254:鄢255:冷256:卓257:花258:仇259:艾260:藍261:都262:鞏263:稽264:井265:練266:仲267:樂268:虞269:卞270:封271:竺272:冼273:原274:官275:衣276:楚277:佟278:栗279:匡280:宗281:應282:臺283:巫284:鞠285:僧286:桑287:荊288:諶289:銀290:揚291:明292:沙293:薄294:伏295:岑296:習297:胥298:保299:和
300:藺
你現在設想,這300個姓氏被攤在一張具有12個小格子的紙上,每個格子有25個姓,第 i個格子對應的那25個性,其序號恰好對應于那些被12除余i的數,即形如12k+i(其中k=0,1,2,…24 )的數,例如,
第1個格子所對應的姓,是以下25個(序號形如12k+1,k=0,1,2,…24),我們排成5行5列【此處要感謝啟功先生】:

第2個格子所對應的姓,是以下25個(序號形如12k+2,k=0,1,2,…24):

類似地,可列出第3個、第4個……第12個格子所對應的25個姓氏,由于劇情需要,我們這里再給出第4個格子所對應的25個姓(其序號形如12k+4,k=0,1,2,…24):

總共恰好有300個姓氏。注意,為了方便起見,更可取的是,會在每個格子里標注一個數字,表明其中各個姓氏所對應的序號被12除的余數。例如,上圖很可能標記為

接下來到了第二步,構造25張小卡片,每張紙上有12個姓氏。現在也許你都可以猜到怎麼構造了。
第 j 張小卡片上的姓氏所對應的序號為 25l +j , 其中 l=0, 1, 2, …,11。
例如,第1張小紙片上的12個姓氏(對應序號為25l+1,其中l=0,1,2,…,11)為

第2張卡上的12個姓氏(對應序號為25l+2,其中l=0,1,2,…,11)為

…………………………………………………………………………………………
類似地,可以造出全部25張卡片。為劇情需要,我們再列出第16張卡片上的12個姓氏(對應序號為25l+16,其中l=0,1,2,…,11)為

現在我們可以保證,第 j 張卡片與第 i 個格子恰好只有一個相同的姓。這里隱含了一個著名的數學定理,數論中有名的 中國剩余定理。 在我們的情況,它相當于說:
設 i,j 是給定的整數,則在1到300這些數中,有且僅有一個整數 x 同時滿足下述兩個條件:x被12除余 i,x被25除余 j。并且這個x可以這樣求得,令y=25i-24j, 則 x=y+300k,其中k是一個適當的整數, 使得x在1到300之間。注意,要緊的是,12與25互素(即能夠同時整除它們的正整數只有1),且300恰好是它們的乘積。
回到我們原來的問題,不難從上述表達式分析得到下述結果:
若 i≥j,則 x 恰好是第 j 張卡片上的第s個姓氏;這里s=(i-j+1)+12 t,其中t是一個適當的整數, 使得s在1到12之間。注意,根據這個分析,我們不需要知道(或記憶)那300個姓氏的序號,只需要知道,i與j,并且從第 j 張卡片就可以讀出 x,它就在第(i-j+1)個位置——在模12的意義下。只要你會做兩位數以內的加減法,會數數,你就會玩這個把戲了!
好了,道具已經備齊,現在我們可以玩把戲了。
比如在本人的情況,當我告訴了你,我的基本信息是i=4, j=16以后,你立即可以算出
i-j+1=4-16+1=﹣11,
從而s=1(取t=1),也就是說,我的姓在第16張卡片(見上圖)的第一個位置,即我跟紫霞同姓(紫霞當然姓林了,因為她的姐姐青霞的全名是林青霞):


好了,我想很多人應該會有興趣嘗試一下了,來吧,實踐出真知。只有當你完全準備好以上12+25=37個道具以后,你才能對姓氏在這300個姓氏中的朋友玩轉這個游戲。(無論如何,雖然這營生成本低,我還是希望各位讀者不要學了這把戲去掙錢。你想想,要是做個簡單的減法都能掙錢,那是不是也來得太容易了!請大家盡量轉發分享這篇文章,提醒世人不要被算命先生故作玄虛的雕蟲小技蒙蔽了!)
按照上述原理,你也可以自行設計不同規格的道具(也許一個更好的選擇是600個姓氏,它分解為兩個互素的數24與25的乘積),只要它們滿足中國剩余定理的互素條件即可。對于需要了解中國剩余定理的朋友,我們將在關于初等數論的系列講座中詳談。若要一睹為快,可以參看這里的一個PPT,從射雕到九章——在天大理學院物理系的通俗報告。當你清楚中國剩余定理的本質以后,應該不難理解我這里簡單陳述而未加證明的結論。我們留給有興趣的朋友吧!
小把戲背后其實藏著美妙的數學,對數學愛好者而言,這何嘗不是一種驚喜?

思考:街頭算命先生往往能夠根據你的生肖猜出你的年齡,知道這是為什麼嗎?
比如說,如果我告訴你我屬豬,而且你又能看出,我不足四十一朵花,又超過三十一枝芽,你猜我多大?
為方便你對照答案,可以告訴你,鄙人與下一版《射雕英雄傳》同歲:

下集
昨日我在本號發表的文章算命是胡扯,猜姓卻不然引發了不少讀者和朋友的反響,他們的反饋讓我對這個小把戲有了進一步認識,因此今天我想趁熱打鐵,繼續跟大家分享我的心得。
昨晚七點多鐘發布完公眾微信號,我最先接到本科同學劉新亮的電話,他現在天津耀華中學教數學。他跟我講,看到這篇推送很高興,因為他下周要去到上小學的孩子班上給講點數學,他正發愁講點什麼內容好。看到這個,他眼前一亮,所以立即給我打了一個電話。我也覺得這個題目不錯,至少準備道具很簡單。一個班最多五六十人(準確地說,需要考慮的只是姓氏的個數,鑒于經常有同姓的同學,所以姓氏個數會更少),他準備十來張卡片就夠了(比如說,56=7*8,7+8=15)。這個游戲尤其適合新生開學的第一堂數學課,當學生與老師都還不熟悉的時候,老師如果通過這個簡單的游戲一下子就猜出學生姓什麼,其形象一下子就高大起來了,同時學生們也立即記住了這個學生的姓氏,再進一步讓學生說出自己的全名,這個印象就深刻多了!想到這些,我當時的得意之情,完全可以用下述圖片來形容:

十點多快要入睡時,又收到了好友劉云朋的一條消息(今天上午也有網友在評論區留言表達了相同的意思,非常感謝!),我瞬間切換到下圖:

云朋兄發給我的消息如下:
第一次知道這樣的把戲,很有趣。我有一個表面上稍不同的理解:假設有100個姓,把它們排成10×10的方陣,然后將同一行的姓填入大圖紙中的同一格,把同一列填入同一小圖紙,于是每種大小圖紙的組合就給出這個矩陣的行指標和列指標,從而標記了既處于指定行又處于指定列的那個元素。他說的方法更簡單了,我們就照他說的方法,來玩一個猜百家姓的把戲。首先,我們選取100個姓氏,如昨天一樣,我們不妨從網絡選取下表
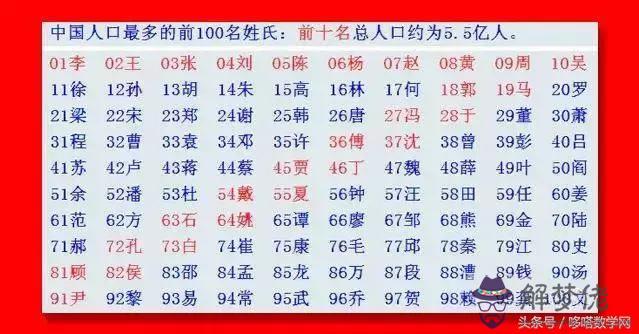
現在每一行的10個姓氏放入一個小格子,為讓蒙蔽效果更好,我們可以將這10個姓氏排成三角垛,例如,第1行的10個姓氏(按照自然順序)排成下述形狀

第2行的10個姓氏(按照自然順序)排成下述形狀

依次類推,一直排到第10行。接下來再將每一列的10個姓氏排在小卡片上,如第1列的10個姓氏為

第2列的10個姓氏為

為劇情需要,我們再給出第6列的10個姓氏

好了,道具20張紙備齊以后,我們就可以來玩猜姓把戲了。比如,你可以確認一下,紫霞的姓(林,表格中對應坐標16)是不是滿足這樣的規律,它恰好在第6列的第2個位置。再如,你也可以驗證金庸《倚天屠龍記》里那位風一樣的女子的姓(楊,表格中對應坐標06)是不是也滿足這樣的規律。


容易發現,與上一篇介紹的用中國剩余定理的方法相比,劉云朋老師(任教于天津大學理學院物理系)介紹的上述方法更簡潔,我反思了一下,發現我們的差別可以這樣理解:
我之前思路是一維的(用數為坐標),而云朋兄這里的思路是二維的(用二個數為坐標)。他進化得比我多些。另一方面,原先的思路由于其復雜性,可能更不容易被外行發現。街頭的各路神仙也許傾向于采取云朋這里的方法。如果學生與老師都熟悉了,當然就不必猜學生的姓名了,這時候可以改為猜學生母親的姓氏(只考慮那些隨父親姓的同學)。

而對于街頭的各路神仙,可以改為猜各位的意中人的姓氏,牛皮可以這樣吹:“你的意中人姓什麼,除了你和你的意中人知道,半仙我也知道!來,我告訴你上天給你安排的姻緣在哪里。”


當來者發現你猜對意中人的姓氏,有了這樣的表情

以后,作為半仙的你還可以借機發揮一下:



到了這個時候,咱們也可以見好就收了!要防著,人家也許有兩個同姓的意中人,還是留給TA自己取舍吧!


作者注1:上一篇有讀者“青青子衿”留言說“我只知道小編愛上了紫霞”,我想更正一下,是作者本人愛上了紫霞(文中圖片均作者自己配好),有本篇為證,也可見本人更早一篇作品,從“三七二十一”到“素數之無窮”。
作者注2:有學數學出生的朋友告訴我,他也曾遇到類似的半仙,也前去拆臺,幸而他從半仙充滿殺氣的眼神中預算到可能要被滅口,這才撿回一條命,終究當上了老總。故事雖然夸張,但在情理之中。建議大家不要當面拆臺(風險太大,在社會上終止問題的可能是拳腳),可以考慮當個娛樂游戲在公眾場合多普及,也許上當的人就少了。

作者注3:留言區有朋友認為,這個把戲用到了數學,有文化內涵,更有美好祝福,憑此哄點小錢也未嘗不可。對此,我倒不反對,但我覺得這主要就是一個娛樂——當然,你要是把人逗樂了,收點錢人家估計也會給。不過,從猜姓把戲中獲得樂趣的,主要是半仙,TA為自己披上了神秘色彩;作為前來測試的人,自己當然知道自己姓什麼,更沒有必要讓半仙知道自己姓什麼。
作者注4:我想強調的是,猜姓與算命不同,前者是有理有據的,而后者則是胡扯、唬人,比如,《飯局也瘋狂》里的大師:




游戲玩一玩無妨,可是坑蒙拐騙就不要參與了,傷感情。圈圈套套,無非圖個財與色。我喜歡開門見山,正大光明,簡單粗暴,像這樣:

或者稍微含蓄一點,又不失果決,像這樣:

如果你了解我,我想你應該猜得到,我期待的回應是怎樣的:

全劇終
關注微信:哆嗒數學網 每天獲得更多數學趣文
新浪微博:http://weibo.com/duodaa
本文來自:解夢佬,原地址:https://www.jiemenglao.com/suanming/356975.html

















