來源：內容由半導體行業觀察（ID：icbank）轉載自公眾號歪睿老哥，作者：申墨 ，謝謝。
1：萊布尼茨的二進制和八卦
在你看本文的這一刻，手機處理器中，正有千萬門級別或者億門的MOS管在關閉和打開，來實現不同的與，或，非的運算。這一切數學基礎都要從數學最基礎的原理來說起。 人類從呱呱墜地開始，耳濡目染最開始就是十進制，小朋友也很容易接受，并可以很快掌握十進制的加減法。 十進制非常通俗易懂，它成為了人類最早的數學基礎。 世界上不同的文明都出現了類似十進制的描述，例如幾千年前的蘇美爾楔形文字，漢字，后來的阿拉伯數字都有十進制的描述。
這個不奇怪，因為人類進化了十根手指頭，用手指頭來數數再自然而不過了。 但是，有人覺得十進制并不完美。 1701年，德國數學家萊布尼茨法國科學院提交并宣讀了他題為《數學科學新論》的研究論文。 在這篇文章中，他提出了用0和1兩個數表示全部數字的方法。 
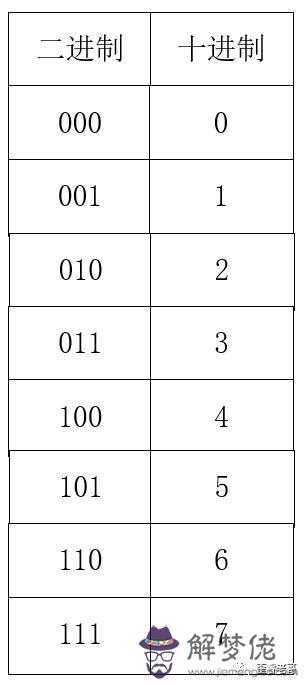如上表所示，每個數字都可以表示一個二進制數。二進制數中只有0和1，沒有其他符號。 魯道夫·奧古斯特公爵研究萊布尼茨的二進制數學后認為二進制數學符合《圣經·創世紀》中的記載，是“上帝的算法”。因為太簡潔了，符合上帝從無到有創建世界的描述。 奧古斯特公爵很喜歡，但是科學院卻把這篇論文給拒了。 當時的法國科學院院長單內認為，看不出這篇論文有什麼用處。論文有什麼用？解決了什麼重大問題？有什麼實際的價值？ 這個思路就一直存在于審稿人的腦海里面，幾百年未曾改變。 那麼有個問題擺在萊布尼茨的面前，二進制有什麼用？ 作為我們300多年后的我們，對于二進制的作用是非常清楚的。但是在當時給二進制找個應用的確是個難題。 但是萊布尼茨作為大數學家，大哲學家。十七世紀的亞里士多德。可以和牛頓爭奪微積分發明權的大佬，肯定不會被這個小問題難住。 但是用了兩年時間，直到1703年萊布尼茨收到白晉所寄的伏羲八卦圖，才發現自己的二進制體系與伏羲八卦圖的一致性。白晉是法國神父，曾經擔任康熙皇帝的數學老師，1697年奉康熙之名回法國招募人才，并與萊布尼茨相識，多次書信來往，白晉由此給萊布尼茨介紹了中國的易經和八卦。 于是，萊布尼茨補充了本項研究意義，并發表在法國皇家科學院院刊上。 標題是《二進制算術闡述-僅僅使用數字0和1兼論其效能及伏羲數字的意義》。 萊布尼茨大神，打算用二進制來描述中國的八卦。 
對于卦象來說，一根長線代表陽爻（陽），兩根短線代表陰爻（陰）。 也就是陰陽。 易經說：道生一，無極變太極；一生二，太極變兩儀；二生三，兩儀變四象；三生萬物，四象旋轉，世界誕生。八卦，正如其名，是對宇宙后續變化的推演。 從伏羲八卦中找到二進制的意義，這個不是什麼戲說。 很多學者論述了，萊布尼茨不是根據八卦而發明二進制，而是發明了二進制才遇到了伏羲八卦，因此本文采用這個說法，而不牽強附會中國的八卦給了萊布尼茨發明二進制的靈感。 對于萊布尼茨這個大數學家來說，二進制只是其很小的數學成就，但是卻是當今信息時代存在的數學基礎。 我們這個信息時代都是建立在二進制上的，在這一點上，萊布尼茨居功至偉。但是，僅僅有二進制是不夠的。 2：布爾運算的真和假
萊布尼茨發明了二進制。此時的二進制還只能像十進制那樣運算，加減乘除。就是換個方式來運算，沒有什麼稀奇。而喬治·布爾則帶了一種運算，那就是布爾代數。 喬治·布爾，1815年出生在英格蘭的林肯，少時家貧，但敏而好學，自學成才，全部的志向都放在數學上。 1847年，布爾出版了《邏輯的數學分析，論演繹推理的演算法》。 從此在數學界名氣大震，并且從“編外人員”到有了正式的教職。 1854年，他又出版了《思維規律的研究，作為邏輯與概率的數學理論的基礎》，其中完滿地討論了這個主題并奠定了所謂的數理邏輯的基礎。為這一學科的發展鋪平了道路。 布爾代數講述內容很多，但其最典型的就是兩種值和三種運算。 布爾在整個計算中，定義兩種值，也就是真和假。1（true），0（false）。 三種基本運算，就是與（AND），或（OR），非（NOT）。 與或非也可以用符號表示： & | ！ 三種符號表示。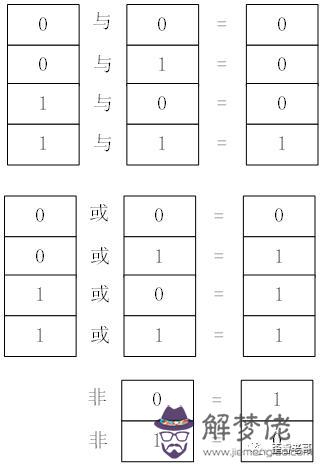
與就是兩個值都為真才為真。或就是兩個值有一個為真就為真。真的非就是假，假的非就是真。 這個就是兩種值，三種運算的含義。有點哲學的意思。 布爾通過研究發現：所有的數字算數運算，都可以用布爾代數化簡成為 0和1的與或非操作。 例如：加法a+b 進位就是a&b，而加完后0位是（a&！b）|（b&！a）也就是可以用與、或、非來表示加減。 
二進制配合布爾代數，能夠表示所有的數學運算。 1864年，布爾去世。但是他發明的這些計算方式，將在100年后得到應用，成為計算機體系中的基本運算。用與、或、非的運算來等價表示加減乘除的運算，這個就是布爾留給后世的財富。3：香農：碩士論文和開關電路
克勞德·艾爾伍德·香農是美國數學家，也是信息論的創始人。 但是，在成為信息論奠基者之前，學生時代的他就發表了一篇劃時代的論文。 1936年，正在讀碩士的香農發表了著名論文《繼電器和開關電路的符號分析》。 在當時能夠實現開關電路的技術方案就是繼電器。 通過磁體通斷打開或者關閉。如果繼電器打開，電流帶來磁場，繼電器合上，電路閉合。如果繼電器關閉，磁場消失，繼電器關閉，電路斷開。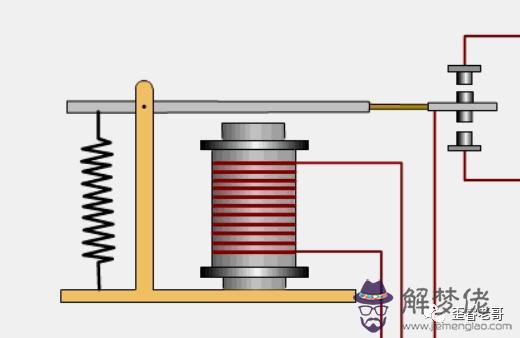
這個開關電路給了香農靈感，配合布爾代數。 香農給出了布爾代數一種物理實現方式。 串聯的開關電路就是布爾運算的與操作，兩個開關a和b都關閉，燈才能亮。 這個電路就是a&b
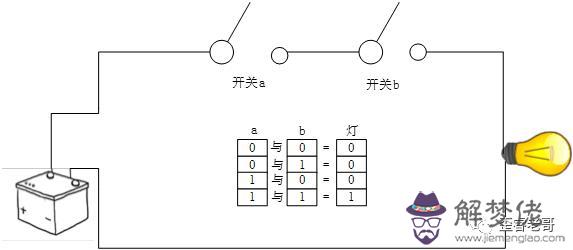而并聯的開關電路就是布爾運算的或操作。兩個開關有一個關閉，燈就會亮。這個電路就是a|b 
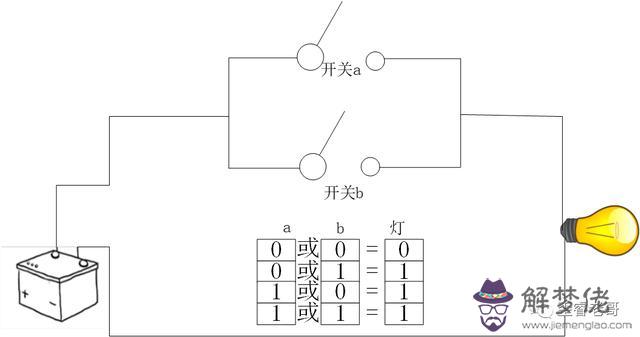是不是看起來簡單極了。 還沒有碩士畢業的香農，奠定了現在數字電路的基礎。布爾計算可以將任何運算化簡為與、或、非。所以不斷重復這兩種電路，就可以通過電路實現任意運算。此時，從萊布尼茨提出了二進制，已經過去了兩百多年，離布爾發表布爾運算也過去接近100年。 終于，香農說，你們的數學表達，我可以用物理電路來實現了。這個就是現代計算機的基石。 哈佛大學的霍華德·加德納（Howard Gardner）教授評價：“這可能是本世紀最重要、最著名的一篇碩士論文。” 4：晶體管和集成電路
1947年，美國物理學家肖克利、巴丁和布拉頓三人合作發明了晶體管。晶體管的誕生，替代了原來的繼電器，電子管等設備。成為了整個信息時代的基礎。 在晶體管發明十年后的1958年，34歲的基爾比加入德州儀器公司。然后有了把多個晶體管放到一起的想法。于是，集成電路誕生了。又過了十二年，1970年，第一個CPU，英特爾4004誕生了。這些基礎都變成如下MOS管的開關電路，下圖就是一個開關電路（gate）。通過控制柵極電壓，實現Source和Drain的通斷。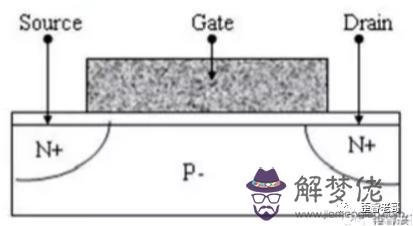
時至今日，芯片的集成度不斷的增加。最新的CPU，GPU，手機處理器等等, 其晶體管的數量都已經超過百億級別。 晶體管數量制程M1160億5nm安培A100540億7nmA14125億5nm麒麟9000153億5nm但是，其內部運行的數學邏輯，仍然是萊布尼茨提出的二進制，布爾發明的布爾計算，和香農描述的開關電路。 一直沒有改變！*免責聲明：本文由作者原創。文章內容系作者個人觀點，半導體行業觀察轉載僅為了傳達一種不同的觀點，不代表半導體行業觀察對該觀點贊同或支持，如果有任何異議，歡迎聯系半導體行業觀察。
今天是《半導體行業觀察》為您分享的第2930內容，歡迎關注。
★從4326億美元窺國產芯片全景
★特斯拉狂奔背后的半導體
★功率半導體材料分析
晶圓｜集成電路｜設備｜汽車芯片｜存儲｜臺積電｜AI｜封裝
本文來自：解夢佬，原地址：https://www.jiemenglao.com/suanming/341657.html
